


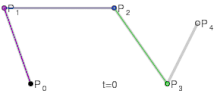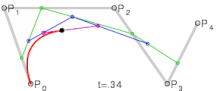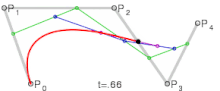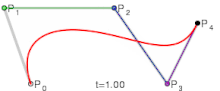

- Articles this image appears in
- Bézier curve
- Creator
- Philip Tregoning ( User:Twirlip)
- Nominator
- froth T
- Support anything but the combined version.
Not sure how this would work; maybe feature all of them as a set and link to the others on each description page?— froth T 02:34, 21 February 2007 (UTC) - Support. You learn quite a lot by looking at the pictures. enochlau ( talk) 03:12, 21 February 2007 (UTC)
- Support all in one or trialsanderrors' arrangement Very informative, maybe combine them into one big diagram or hve 4 FPs from 1 FPC nom? -- antilived T | C | G 03:32, 21 February 2007 (UTC)
- Support No idea WTF it is but one word sweet Voshvoshka 05:07, 21 February 2007 (UTC)
- Strong support I'd say combine into a single animation. Why not? Debivort 05:22, 21 February 2007 (UTC)
- Conditional support - if we can get this into one image - needs to function as PotD on the front page, some day. (The linear version could be left out... ;-) --
Janke |
Talk
09:03, 21 February 2007 (UTC)
- I say use just the quadratic on the front page and have it as a set.. I'll find/design the set template after classes today (or during classes if I get bored :P) --
froth
T
13:46, 21 February 2007 (UTC)
- How did we end up doing that fractal series a couple months ago?
Debivort
17:22, 21 February 2007 (UTC)
- I don't know, but that's exactly what I was thinking of --
froth
T
00:35, 22 February 2007 (UTC)
- This is how Raven4x4x handled it. tiZom (2¢) 02:56, 22 February 2007 (UTC)
- Oh, and I support the full nomination as-is (all 4 separately as a set). :o)
tiZom
(2¢)
02:58, 22 February 2007 (UTC)
- BTW, the fractals haven't shown up as POTD yet.
howcheng {
chat}
05:54, 23 February 2007 (UTC)
- I guess when the fractals go up we can do something like the thumbnail of the outermost image, the caption, and a "Click here to view the series" like the animation link. Then we can do the same thing for the beziers: have a frame of one of the animations (quadratic probably, maybe around t=.55?), the caption, and "Click here to view the series". -- froth T 18:44, 23 February 2007 (UTC)
- BTW, the fractals haven't shown up as POTD yet.
howcheng {
chat}
05:54, 23 February 2007 (UTC)
- I don't know, but that's exactly what I was thinking of --
froth
T
00:35, 22 February 2007 (UTC)
- How did we end up doing that fractal series a couple months ago?
Debivort
17:22, 21 February 2007 (UTC)
- I say use just the quadratic on the front page and have it as a set.. I'll find/design the set template after classes today (or during classes if I get bored :P) --
froth
T
13:46, 21 February 2007 (UTC)
- Strong support - Definitely. So that's how it's done! Perhaps just pic. 3 or 4 on its own, perhaps the last three combined? Mrug 2 13:28, 21 February 2007 (UTC)
- while #3 is pretty straightforward, I think #2 is essential also. Debivort 17:22, 21 February 2007 (UTC)
- Support.-- Dwaipayan ( talk) 04:52, 22 February 2007 (UTC)
- Support and Comment, I don't have the technology but I'd like to see one gif that is a 2x2 rectangle with time synced (putting "linear" on it's side and adding white space where needed so all four exemplars are the same dimensions). Can someone make something like this? -- Cody.Pope 05:19, 22 February 2007 (UTC)
- Maybe have 5 sets of identical points and apply each degree of bézier curve to each of them (ie. linear for the first, which would be sharp zig zag lines, etc.)? -- antilived T | C | G 08:06, 22 February 2007 (UTC)
- Support These make quite interesting animations that aren't half as scary as the maths that goes with them. I think Antilived's idea that they should all have five points in a set pattern and then apply the different degree of curve to them would be good, perhaps should avoid too many right angles though. Terri G 12:28, 22 February 2007 (UTC)
- Support Holy cow, THIS is how Bezier curves work? I've always been confounded by these things, and here we are, a single animation that explains it all. Brilliant! -- Golbez 22:19, 22 February 2007 (UTC)
- Support. You know, I've never had a problem using Bezier curves in Illustrator in Inkscape ... all the article did was make it a lot more confusing. :) howcheng { chat} 05:53, 23 February 2007 (UTC)
- Support, holy crap this is one of the most intuitively informative images I've seen on wikipedia. Night Gyr ( talk/ Oy) 11:36, 23 February 2007 (UTC)
- Support cubic. Quartic is slightly too complicated to follow, and also fairly uncommon. Quadratic is too simple.
ed g2s •
talk
16:31, 23 February 2007 (UTC)
- Uncommon? I thought that beziers were usually on the order of dozens of degrees for like edge tracing/smoothing, and that these were just for demonstration of how it works. Also, multiple degrees are important to show how the algorithm scales- otherwise it wouldn't be so "intuitively informative" so we shouldn't just feature one of them. And I have no trouble at all tracking quartic, although the one after the one after quartic is a little disorienting -- froth T 18:28, 23 February 2007 (UTC)
- Support all, but would it be possible to make them all the same size so they can be presented as a set? ~ trialsanderrors 19:18, 23 February 2007 (UTC)
- Neutral for now. I agree with Janke that the set should be fitted in a single image. Also, a little more attention should be given to the details, like the position (not over the lines, please) and size of the labels, and the thickness of the lines, which should be consistent in all images. It is a nice and quite clear animation but can be improved.
Alvesgaspar
00:19, 24 February 2007 (UTC)
- The size of the labels and thinkness of the lines are consistent in each one.. -- froth T 07:17, 24 February 2007 (UTC)
- Support. Very cool. I like Antilived's idea (as much as I can understand it, which isn't much), and the Mendelbrot set is procedure should be used as a precedent.-- Here T oHelp 19:29, 24 February 2007 (UTC)
Strong Oppose, Strong support all-in-one version — I can see right now that my vote isn't going to change the outcome of this candidacy, but I think these images, even as animations, are FAR too small. We need higher resolution animations. Image:Bezier linear anim.gif would be a record for the smallest FP ever by a long shot. These are excellent animations, but they are incredibly tiny. ♠ SG →Talk 03:54, 25 February 2007 (UTC)
- But do you actually gain any more information from a higher resolution image? These images could well have infinite spatial and temporal resolution with up and coming stuffs like svg animation but is it absolutely neccessary for them to be a few megabytes big just to have more than 1k pixels for one side? --
antilived
T |
C |
G
04:38, 25 February 2007 (UTC)
- If possible, svg animations would be really cool. It also means that the stills in the article could be vectorized. Still, there's nothing wrong with the rasters.--
Here
T
oHelp
14:12, 25 February 2007 (UTC)
- SVG animation is supported in the standard but firefox and IE won't render it -- froth T 06:31, 26 February 2007 (UTC)
- If possible, svg animations would be really cool. It also means that the stills in the article could be vectorized. Still, there's nothing wrong with the rasters.--
Here
T
oHelp
14:12, 25 February 2007 (UTC)
- Excellent work on the new version! Not only were all of the animations added into one, but they were also made much larger than previously. As it stands, I would prefer that THAT particular image gain featured picture status, while the other versions (though I'd still like to see them larger) remain to be used in the article as they are and be linked to from the all-in-one version's description page. ♠ SG →Talk 03:21, 26 February 2007 (UTC)
- Hi there. Glad you all (well most of you:) liked my animations. I actually created them for another web page (that has never seen the light of day), and then uploaded them to wikipedia/wikicommons later. They were created using a rather hairy
Bash script that outputs another script that invokes
ImageMagick to create the
GIFs and
PNGs. I can resize, change colours, move the points around etc. pretty easily. About the only thing I can't do is increase the number of frames in the animations by much, because then the argument list gets too long! I think most complaints were about the size of the images and that they are different sizes. I created them for the Bezier Curve wiki page and not to a be Featured Picture, so I was trying to keep file sizes a small as possible while still getting the point across. I'll knock together another version, addressing these points. Oh, and if anyone wants the Bash script, they're welcome to it. --
Twirlip
17:24, 25 February 2007 (UTC)
- You should put it on the talk page for the images. It's great when we get not only great diagrams, but source code for them too.
Night Gyr (
talk/
Oy)
22:03, 25 February 2007 (UTC)
- Here's an image of 1st to fourth order curves. They don't work very well any bigger than this without increasing the number of frames in the animation, which I have problems with. I tried to keep this image true to to the ones on the Bezier Curve page, because that's what it's showcasing. Bash script on its way tomorrow... --
Twirlip
00:18, 26 February 2007 (UTC)
- I don't like the all in one. It's too busy and confusing. Just making four images of the same width would clean it up fine.
Night Gyr (
talk/
Oy)
02:48, 26 February 2007 (UTC)
- I agree, I'd much rather have separate ones of the same width. Combining the images would be highly unusual and quite unnecessary. Great work twirl, keep it up
- I've now put up some slightly bigger images an the originals (about the same size as they are in the combined image), and made them the all the same dimensions. Hopefully they'll make their way over from the commons soon... -- Twirlip 19:48, 28 February 2007 (UTC)
- I agree, I'd much rather have separate ones of the same width. Combining the images would be highly unusual and quite unnecessary. Great work twirl, keep it up
- I don't like the all in one. It's too busy and confusing. Just making four images of the same width would clean it up fine.
Night Gyr (
talk/
Oy)
02:48, 26 February 2007 (UTC)
- Here's an image of 1st to fourth order curves. They don't work very well any bigger than this without increasing the number of frames in the animation, which I have problems with. I tried to keep this image true to to the ones on the Bezier Curve page, because that's what it's showcasing. Bash script on its way tomorrow... --
Twirlip
00:18, 26 February 2007 (UTC)
- You should put it on the talk page for the images. It's great when we get not only great diagrams, but source code for them too.
Night Gyr (
talk/
Oy)
22:03, 25 February 2007 (UTC)
-- froth T 06:34, 26 February 2007 (UTC)
- Support I always wondered what the distinction was between these different types? I once bought S/N 000136 of the very first Adobe Illustrator a long time ago (bezier curves). Now I know how the others work. Very nice! Greg L 06:35, 26 February 2007 (UTC)
Oppose, Support — While the images are very pretty, I don't think they're very effective at giving an intuitive idea of how a Bezier curve is constructed. The intermediate line segments don't seem to add anything of substance to the pictures - they don't seem to add any information. And the article doesn't give a good explanation of their purpose either. Take the quadratic case, for instance: I can choose a point P1-prime, distinct from and further out from the original P1, and arrange it so that the green line segment is tangential to the red Bezier curve for every intermediate state in that case as well. So, by this sort of geometric illustration, nothing about P1 uniquely defines the curve - two distinct points P1 can define the same curve. There needs to be more information in the picture; for instance, what determines the point along the green segment where it's tangential to the curve? -- Paul 17:12, 26 February 2007 (UTC)- I can see an argument that given three points P0, P1, P2, the Bézier curve needs to be uniquely defined, but how does that translate into an argument that that curve has to be distinct from one defined by P0', P1, P2? Also, the location of the tangent point on the green line is quite obviously defined by t. I don't even need to description to see that. ~
trialsanderrors
19:02, 26 February 2007 (UTC)
- In answer to your first question: it doesn't. You're right, and I didn't articulate my point quite as well as I would've liked to. I was only trying to state the first part of your question: that given three points (...), the Bézier curve needs to be uniquely defined. But I don't think that's illustrated very well with the graphical technique used. The information that seems to be missing are the visual factors determining the enpoints, Q1 and Q2, of the green line segment. Without that info, the choice of Q1 and Q2 seems to be arbitrary for any particluar value of the parameter t, and we could trace-out any curve at all in the absence of this info. But then, maybe I'm splitting hairs here. After all, the position of (for instance) Q1 along the line segment P1-P2 would be decided by another parametric equation that's almost a projection of the original, and that would be difficult to illustrate in a more intuitive fashion. Perhaps the most important aspects of this have been successfully demonstrated intuitively, and I'm just trying to hash-out the details for myself. -- Paul 22:38, 26 February 2007 (UTC)
- By the way, that would be P0, P1, P2, not P1, P2, P3 (have another look at the diagram for the quadratic case). Perhaps that caused some of the confusion? --
Paul
22:38, 26 February 2007 (UTC)
- Labeling fixed, thanks. The endpoints of the green line are defined in the same way as the pencil point on the green line, it moves from Q1 to Q2 at linear speed (i.e. it replicates the movement of the linear Bézier). That's the same principle that governs every single movement of a point along a line in all versions. I see nothing arbitrary about this. Simplified, if the starting point is 0 and the endpoint is 1, the position of the moving point at time t is t. (To make it clear, I don't have any prior knowledge of Béziers nor did I read the article in detail. The algorithm is perfectly simple and obvious from looking at the animation.) ~
trialsanderrors
22:55, 26 February 2007 (UTC)
- I totally missed the fact of all the motion being linear / constant-speed. *smacks forehead* (and yes, it's very obvious in retrospect) -- Paul 16:12, 1 March 2007 (UTC)
- Labeling fixed, thanks. The endpoints of the green line are defined in the same way as the pencil point on the green line, it moves from Q1 to Q2 at linear speed (i.e. it replicates the movement of the linear Bézier). That's the same principle that governs every single movement of a point along a line in all versions. I see nothing arbitrary about this. Simplified, if the starting point is 0 and the endpoint is 1, the position of the moving point at time t is t. (To make it clear, I don't have any prior knowledge of Béziers nor did I read the article in detail. The algorithm is perfectly simple and obvious from looking at the animation.) ~
trialsanderrors
22:55, 26 February 2007 (UTC)
- The actual algorithm for computing a bezier curve doesn't have to involve tangency. Take the quadratic one for example. The bezier curve is defined by the a point moving through space. This point is the midpoint of the green line. As time goes by, the endpoints of the green line go from P0 to P1 and from P1 to P2 respectively, at a rate of distance/time. For higher degrees of curve, P0 P1 and P2 aren't defined by the grey lines anymore- they're defined by a chain of parent functions that go all the way up to the grey lines through the same algorithm. So these intermediate line segments show how Bezier curves are algorithmically constructed, although mathematically the curve can still be expressed by
- I can see an argument that given three points P0, P1, P2, the Bézier curve needs to be uniquely defined, but how does that translate into an argument that that curve has to be distinct from one defined by P0', P1, P2? Also, the location of the tangent point on the green line is quite obviously defined by t. I don't even need to description to see that. ~
trialsanderrors
19:02, 26 February 2007 (UTC)
- --
froth
T
20:43, 26 February 2007 (UTC)
- It's not the midpoint of the green line, the black dot (i.e., the "pencil") moves along the green line governed by the value of t. At t = 0, it's at the start of the green line, at t = 1, it's at the end. I haven't looked at the maths involved, but from eyeballing it's very plausible that it's always a tangent point. ~
trialsanderrors
21:20, 26 February 2007 (UTC)
- Ah yes of course. I don't know what I was thinking -- froth T 01:07, 27 February 2007 (UTC)
- It's not the midpoint of the green line, the black dot (i.e., the "pencil") moves along the green line governed by the value of t. At t = 0, it's at the start of the green line, at t = 1, it's at the end. I haven't looked at the maths involved, but from eyeballing it's very plausible that it's always a tangent point. ~
trialsanderrors
21:20, 26 February 2007 (UTC)
- I've rescinded my original opposition. I think this does a damn good job at illustrating and giving an intuitive feel for how a bezier curve is constructed, in the ways that matter most. My initial objection was too pedantic. -- Paul 22:45, 26 February 2007 (UTC)
- --
froth
T
20:43, 26 February 2007 (UTC)
- Support The all in one version. How exactly are votes going to be tallied, since it isn't really clear which of the several versions some people are voting for?-- Lewk_of_S e rthic contrib talk 23:37, 26 February 2007 (UTC)
- Support all Tomer T 22:04, 24 March 2007 (UTC)
1.
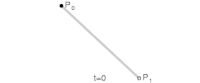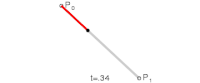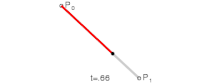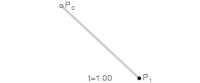
|
2.

|
3.

|
4.

|
| Bézier curves: 1. linear; 2. quadratic; 3. cubic; 4. quartic. | |
Yep, exactly. More input required... MER-C 09:03, 28 February 2007 (UTC)
- support any solution. It might be good to outline the front-running possibilities though. Debivort 09:31, 28 February 2007 (UTC)
- Support, per my original vote, also, I'm comfy with any consensus choice. The combo image needs a little tweaking, the Po is touching the line in the first image. Having seen the combo, I really think the Quartic would be best as FP, with links to the others. --
Janke |
Talk
09:47, 28 February 2007 (UTC)
- More comments: The combo above looks good, but the animations are not synchronized - but I don't know if that really matters. The linear could be drawn out a little, to fill the empty space in the upper left quadrant. --
Janke |
Talk
08:01, 1 March 2007 (UTC)
- They appear synchronized to me. Maybe it's your browser --
froth
T
23:44, 1 March 2007 (UTC)
- They can be asynchronous the first time you download the page, since animated gifs start immediately after downloading. The second time the files are already in your browser cache, so they should start synchronously. ~ trialsanderrors 21:46, 6 March 2007 (UTC)
- They appear synchronized to me. Maybe it's your browser --
froth
T
23:44, 1 March 2007 (UTC)
- More comments: The combo above looks good, but the animations are not synchronized - but I don't know if that really matters. The linear could be drawn out a little, to fill the empty space in the upper left quadrant. --
Janke |
Talk
08:01, 1 March 2007 (UTC)
Support combined version. Noclip 19:44, 28 February 2007 (UTC)
- Support trialsanderrors version. Noclip 03:56, 1 March 2007 (UTC)
- Comment I arranged the new versions in a table and Support that arrangement. ~ trialsanderrors 23:17, 28 February 2007 (UTC)
- Support the same-sized but separate images. Feature them all. -- froth T 23:44, 1 March 2007 (UTC)
- Comment - Please don't put the label "P1" over the segment - Alvesgaspar 21:47, 2 March 2007 (UTC)
- Strong support "All together now" version, wow, I am learning. HighInBC(Need help? Ask me) 19:11, 10 March 2007 (UTC)
- Oppose set, per my comment above - Alvesgaspar 13:07, 11 March 2007 (UTC)
- Support I support the combined image.-- Paul 17:50, 12 March 2007 (UTC)
- Q So is this going to be our first featured set? ~
trialsanderrors
17:32, 15 March 2007 (UTC)
- No, look at the description on
this page --
froth
t
18:49, 23 March 2007 (UTC)
- See the discussion and the new template on the talk page. ~ trialsanderrors 19:11, 23 March 2007 (UTC)
- No, look at the description on
this page --
froth
t
18:49, 23 March 2007 (UTC)
- Still support cubic. Higher order curves a rarely used. "Quadratic and cubic Bézier curves are most common; higher degree curves are more expensive to evaluate. When more complex shapes are needed, low order Bézier curves are patched together." ed g2s • talk 23:39, 19 March 2007 (UTC)
- Support as a set, the images are not used together in the article. -- KFP ( talk | contribs) 13:39, 28 March 2007 (UTC)
- Support the all-in-one version. Very, very nice. And what an excellent visualization. We need a lot more images like this. -- Cyde Weys 01:07, 1 April 2007 (UTC)
- Comment. The article where these images appear, Bézier curve, would probably have to be refactored if the combined version was promoted. -- KFP ( talk | contribs) 10:48, 2 April 2007 (UTC)
- Support. My preference is for the four curves to be promoted as a set but kept as separate images. One can be selected as representative of the set when it comes to Main Page appearances etc. Pstuart84 Talk 15:42, 2 April 2007 (UTC)
Promoted as a set, with Image:Bézier 3 big.gif as main image. -- KFP ( talk | contribs) 10:06, 3 April 2007 (UTC)





- Articles this image appears in
- Bézier curve
- Creator
- Philip Tregoning ( User:Twirlip)
- Nominator
- froth T
- Support anything but the combined version.
Not sure how this would work; maybe feature all of them as a set and link to the others on each description page?— froth T 02:34, 21 February 2007 (UTC) - Support. You learn quite a lot by looking at the pictures. enochlau ( talk) 03:12, 21 February 2007 (UTC)
- Support all in one or trialsanderrors' arrangement Very informative, maybe combine them into one big diagram or hve 4 FPs from 1 FPC nom? -- antilived T | C | G 03:32, 21 February 2007 (UTC)
- Support No idea WTF it is but one word sweet Voshvoshka 05:07, 21 February 2007 (UTC)
- Strong support I'd say combine into a single animation. Why not? Debivort 05:22, 21 February 2007 (UTC)
- Conditional support - if we can get this into one image - needs to function as PotD on the front page, some day. (The linear version could be left out... ;-) --
Janke |
Talk
09:03, 21 February 2007 (UTC)
- I say use just the quadratic on the front page and have it as a set.. I'll find/design the set template after classes today (or during classes if I get bored :P) --
froth
T
13:46, 21 February 2007 (UTC)
- How did we end up doing that fractal series a couple months ago?
Debivort
17:22, 21 February 2007 (UTC)
- I don't know, but that's exactly what I was thinking of --
froth
T
00:35, 22 February 2007 (UTC)
- This is how Raven4x4x handled it. tiZom (2¢) 02:56, 22 February 2007 (UTC)
- Oh, and I support the full nomination as-is (all 4 separately as a set). :o)
tiZom
(2¢)
02:58, 22 February 2007 (UTC)
- BTW, the fractals haven't shown up as POTD yet.
howcheng {
chat}
05:54, 23 February 2007 (UTC)
- I guess when the fractals go up we can do something like the thumbnail of the outermost image, the caption, and a "Click here to view the series" like the animation link. Then we can do the same thing for the beziers: have a frame of one of the animations (quadratic probably, maybe around t=.55?), the caption, and "Click here to view the series". -- froth T 18:44, 23 February 2007 (UTC)
- BTW, the fractals haven't shown up as POTD yet.
howcheng {
chat}
05:54, 23 February 2007 (UTC)
- I don't know, but that's exactly what I was thinking of --
froth
T
00:35, 22 February 2007 (UTC)
- How did we end up doing that fractal series a couple months ago?
Debivort
17:22, 21 February 2007 (UTC)
- I say use just the quadratic on the front page and have it as a set.. I'll find/design the set template after classes today (or during classes if I get bored :P) --
froth
T
13:46, 21 February 2007 (UTC)
- Strong support - Definitely. So that's how it's done! Perhaps just pic. 3 or 4 on its own, perhaps the last three combined? Mrug 2 13:28, 21 February 2007 (UTC)
- while #3 is pretty straightforward, I think #2 is essential also. Debivort 17:22, 21 February 2007 (UTC)
- Support.-- Dwaipayan ( talk) 04:52, 22 February 2007 (UTC)
- Support and Comment, I don't have the technology but I'd like to see one gif that is a 2x2 rectangle with time synced (putting "linear" on it's side and adding white space where needed so all four exemplars are the same dimensions). Can someone make something like this? -- Cody.Pope 05:19, 22 February 2007 (UTC)
- Maybe have 5 sets of identical points and apply each degree of bézier curve to each of them (ie. linear for the first, which would be sharp zig zag lines, etc.)? -- antilived T | C | G 08:06, 22 February 2007 (UTC)
- Support These make quite interesting animations that aren't half as scary as the maths that goes with them. I think Antilived's idea that they should all have five points in a set pattern and then apply the different degree of curve to them would be good, perhaps should avoid too many right angles though. Terri G 12:28, 22 February 2007 (UTC)
- Support Holy cow, THIS is how Bezier curves work? I've always been confounded by these things, and here we are, a single animation that explains it all. Brilliant! -- Golbez 22:19, 22 February 2007 (UTC)
- Support. You know, I've never had a problem using Bezier curves in Illustrator in Inkscape ... all the article did was make it a lot more confusing. :) howcheng { chat} 05:53, 23 February 2007 (UTC)
- Support, holy crap this is one of the most intuitively informative images I've seen on wikipedia. Night Gyr ( talk/ Oy) 11:36, 23 February 2007 (UTC)
- Support cubic. Quartic is slightly too complicated to follow, and also fairly uncommon. Quadratic is too simple.
ed g2s •
talk
16:31, 23 February 2007 (UTC)
- Uncommon? I thought that beziers were usually on the order of dozens of degrees for like edge tracing/smoothing, and that these were just for demonstration of how it works. Also, multiple degrees are important to show how the algorithm scales- otherwise it wouldn't be so "intuitively informative" so we shouldn't just feature one of them. And I have no trouble at all tracking quartic, although the one after the one after quartic is a little disorienting -- froth T 18:28, 23 February 2007 (UTC)
- Support all, but would it be possible to make them all the same size so they can be presented as a set? ~ trialsanderrors 19:18, 23 February 2007 (UTC)
- Neutral for now. I agree with Janke that the set should be fitted in a single image. Also, a little more attention should be given to the details, like the position (not over the lines, please) and size of the labels, and the thickness of the lines, which should be consistent in all images. It is a nice and quite clear animation but can be improved.
Alvesgaspar
00:19, 24 February 2007 (UTC)
- The size of the labels and thinkness of the lines are consistent in each one.. -- froth T 07:17, 24 February 2007 (UTC)
- Support. Very cool. I like Antilived's idea (as much as I can understand it, which isn't much), and the Mendelbrot set is procedure should be used as a precedent.-- Here T oHelp 19:29, 24 February 2007 (UTC)
Strong Oppose, Strong support all-in-one version — I can see right now that my vote isn't going to change the outcome of this candidacy, but I think these images, even as animations, are FAR too small. We need higher resolution animations. Image:Bezier linear anim.gif would be a record for the smallest FP ever by a long shot. These are excellent animations, but they are incredibly tiny. ♠ SG →Talk 03:54, 25 February 2007 (UTC)
- But do you actually gain any more information from a higher resolution image? These images could well have infinite spatial and temporal resolution with up and coming stuffs like svg animation but is it absolutely neccessary for them to be a few megabytes big just to have more than 1k pixels for one side? --
antilived
T |
C |
G
04:38, 25 February 2007 (UTC)
- If possible, svg animations would be really cool. It also means that the stills in the article could be vectorized. Still, there's nothing wrong with the rasters.--
Here
T
oHelp
14:12, 25 February 2007 (UTC)
- SVG animation is supported in the standard but firefox and IE won't render it -- froth T 06:31, 26 February 2007 (UTC)
- If possible, svg animations would be really cool. It also means that the stills in the article could be vectorized. Still, there's nothing wrong with the rasters.--
Here
T
oHelp
14:12, 25 February 2007 (UTC)
- Excellent work on the new version! Not only were all of the animations added into one, but they were also made much larger than previously. As it stands, I would prefer that THAT particular image gain featured picture status, while the other versions (though I'd still like to see them larger) remain to be used in the article as they are and be linked to from the all-in-one version's description page. ♠ SG →Talk 03:21, 26 February 2007 (UTC)
- Hi there. Glad you all (well most of you:) liked my animations. I actually created them for another web page (that has never seen the light of day), and then uploaded them to wikipedia/wikicommons later. They were created using a rather hairy
Bash script that outputs another script that invokes
ImageMagick to create the
GIFs and
PNGs. I can resize, change colours, move the points around etc. pretty easily. About the only thing I can't do is increase the number of frames in the animations by much, because then the argument list gets too long! I think most complaints were about the size of the images and that they are different sizes. I created them for the Bezier Curve wiki page and not to a be Featured Picture, so I was trying to keep file sizes a small as possible while still getting the point across. I'll knock together another version, addressing these points. Oh, and if anyone wants the Bash script, they're welcome to it. --
Twirlip
17:24, 25 February 2007 (UTC)
- You should put it on the talk page for the images. It's great when we get not only great diagrams, but source code for them too.
Night Gyr (
talk/
Oy)
22:03, 25 February 2007 (UTC)
- Here's an image of 1st to fourth order curves. They don't work very well any bigger than this without increasing the number of frames in the animation, which I have problems with. I tried to keep this image true to to the ones on the Bezier Curve page, because that's what it's showcasing. Bash script on its way tomorrow... --
Twirlip
00:18, 26 February 2007 (UTC)
- I don't like the all in one. It's too busy and confusing. Just making four images of the same width would clean it up fine.
Night Gyr (
talk/
Oy)
02:48, 26 February 2007 (UTC)
- I agree, I'd much rather have separate ones of the same width. Combining the images would be highly unusual and quite unnecessary. Great work twirl, keep it up
- I've now put up some slightly bigger images an the originals (about the same size as they are in the combined image), and made them the all the same dimensions. Hopefully they'll make their way over from the commons soon... -- Twirlip 19:48, 28 February 2007 (UTC)
- I agree, I'd much rather have separate ones of the same width. Combining the images would be highly unusual and quite unnecessary. Great work twirl, keep it up
- I don't like the all in one. It's too busy and confusing. Just making four images of the same width would clean it up fine.
Night Gyr (
talk/
Oy)
02:48, 26 February 2007 (UTC)
- Here's an image of 1st to fourth order curves. They don't work very well any bigger than this without increasing the number of frames in the animation, which I have problems with. I tried to keep this image true to to the ones on the Bezier Curve page, because that's what it's showcasing. Bash script on its way tomorrow... --
Twirlip
00:18, 26 February 2007 (UTC)
- You should put it on the talk page for the images. It's great when we get not only great diagrams, but source code for them too.
Night Gyr (
talk/
Oy)
22:03, 25 February 2007 (UTC)
-- froth T 06:34, 26 February 2007 (UTC)
- Support I always wondered what the distinction was between these different types? I once bought S/N 000136 of the very first Adobe Illustrator a long time ago (bezier curves). Now I know how the others work. Very nice! Greg L 06:35, 26 February 2007 (UTC)
Oppose, Support — While the images are very pretty, I don't think they're very effective at giving an intuitive idea of how a Bezier curve is constructed. The intermediate line segments don't seem to add anything of substance to the pictures - they don't seem to add any information. And the article doesn't give a good explanation of their purpose either. Take the quadratic case, for instance: I can choose a point P1-prime, distinct from and further out from the original P1, and arrange it so that the green line segment is tangential to the red Bezier curve for every intermediate state in that case as well. So, by this sort of geometric illustration, nothing about P1 uniquely defines the curve - two distinct points P1 can define the same curve. There needs to be more information in the picture; for instance, what determines the point along the green segment where it's tangential to the curve? -- Paul 17:12, 26 February 2007 (UTC)- I can see an argument that given three points P0, P1, P2, the Bézier curve needs to be uniquely defined, but how does that translate into an argument that that curve has to be distinct from one defined by P0', P1, P2? Also, the location of the tangent point on the green line is quite obviously defined by t. I don't even need to description to see that. ~
trialsanderrors
19:02, 26 February 2007 (UTC)
- In answer to your first question: it doesn't. You're right, and I didn't articulate my point quite as well as I would've liked to. I was only trying to state the first part of your question: that given three points (...), the Bézier curve needs to be uniquely defined. But I don't think that's illustrated very well with the graphical technique used. The information that seems to be missing are the visual factors determining the enpoints, Q1 and Q2, of the green line segment. Without that info, the choice of Q1 and Q2 seems to be arbitrary for any particluar value of the parameter t, and we could trace-out any curve at all in the absence of this info. But then, maybe I'm splitting hairs here. After all, the position of (for instance) Q1 along the line segment P1-P2 would be decided by another parametric equation that's almost a projection of the original, and that would be difficult to illustrate in a more intuitive fashion. Perhaps the most important aspects of this have been successfully demonstrated intuitively, and I'm just trying to hash-out the details for myself. -- Paul 22:38, 26 February 2007 (UTC)
- By the way, that would be P0, P1, P2, not P1, P2, P3 (have another look at the diagram for the quadratic case). Perhaps that caused some of the confusion? --
Paul
22:38, 26 February 2007 (UTC)
- Labeling fixed, thanks. The endpoints of the green line are defined in the same way as the pencil point on the green line, it moves from Q1 to Q2 at linear speed (i.e. it replicates the movement of the linear Bézier). That's the same principle that governs every single movement of a point along a line in all versions. I see nothing arbitrary about this. Simplified, if the starting point is 0 and the endpoint is 1, the position of the moving point at time t is t. (To make it clear, I don't have any prior knowledge of Béziers nor did I read the article in detail. The algorithm is perfectly simple and obvious from looking at the animation.) ~
trialsanderrors
22:55, 26 February 2007 (UTC)
- I totally missed the fact of all the motion being linear / constant-speed. *smacks forehead* (and yes, it's very obvious in retrospect) -- Paul 16:12, 1 March 2007 (UTC)
- Labeling fixed, thanks. The endpoints of the green line are defined in the same way as the pencil point on the green line, it moves from Q1 to Q2 at linear speed (i.e. it replicates the movement of the linear Bézier). That's the same principle that governs every single movement of a point along a line in all versions. I see nothing arbitrary about this. Simplified, if the starting point is 0 and the endpoint is 1, the position of the moving point at time t is t. (To make it clear, I don't have any prior knowledge of Béziers nor did I read the article in detail. The algorithm is perfectly simple and obvious from looking at the animation.) ~
trialsanderrors
22:55, 26 February 2007 (UTC)
- The actual algorithm for computing a bezier curve doesn't have to involve tangency. Take the quadratic one for example. The bezier curve is defined by the a point moving through space. This point is the midpoint of the green line. As time goes by, the endpoints of the green line go from P0 to P1 and from P1 to P2 respectively, at a rate of distance/time. For higher degrees of curve, P0 P1 and P2 aren't defined by the grey lines anymore- they're defined by a chain of parent functions that go all the way up to the grey lines through the same algorithm. So these intermediate line segments show how Bezier curves are algorithmically constructed, although mathematically the curve can still be expressed by
- I can see an argument that given three points P0, P1, P2, the Bézier curve needs to be uniquely defined, but how does that translate into an argument that that curve has to be distinct from one defined by P0', P1, P2? Also, the location of the tangent point on the green line is quite obviously defined by t. I don't even need to description to see that. ~
trialsanderrors
19:02, 26 February 2007 (UTC)
- --
froth
T
20:43, 26 February 2007 (UTC)
- It's not the midpoint of the green line, the black dot (i.e., the "pencil") moves along the green line governed by the value of t. At t = 0, it's at the start of the green line, at t = 1, it's at the end. I haven't looked at the maths involved, but from eyeballing it's very plausible that it's always a tangent point. ~
trialsanderrors
21:20, 26 February 2007 (UTC)
- Ah yes of course. I don't know what I was thinking -- froth T 01:07, 27 February 2007 (UTC)
- It's not the midpoint of the green line, the black dot (i.e., the "pencil") moves along the green line governed by the value of t. At t = 0, it's at the start of the green line, at t = 1, it's at the end. I haven't looked at the maths involved, but from eyeballing it's very plausible that it's always a tangent point. ~
trialsanderrors
21:20, 26 February 2007 (UTC)
- I've rescinded my original opposition. I think this does a damn good job at illustrating and giving an intuitive feel for how a bezier curve is constructed, in the ways that matter most. My initial objection was too pedantic. -- Paul 22:45, 26 February 2007 (UTC)
- --
froth
T
20:43, 26 February 2007 (UTC)
- Support The all in one version. How exactly are votes going to be tallied, since it isn't really clear which of the several versions some people are voting for?-- Lewk_of_S e rthic contrib talk 23:37, 26 February 2007 (UTC)
- Support all Tomer T 22:04, 24 March 2007 (UTC)
1.

|
2.

|
3.

|
4.

|
| Bézier curves: 1. linear; 2. quadratic; 3. cubic; 4. quartic. | |
Yep, exactly. More input required... MER-C 09:03, 28 February 2007 (UTC)
- support any solution. It might be good to outline the front-running possibilities though. Debivort 09:31, 28 February 2007 (UTC)
- Support, per my original vote, also, I'm comfy with any consensus choice. The combo image needs a little tweaking, the Po is touching the line in the first image. Having seen the combo, I really think the Quartic would be best as FP, with links to the others. --
Janke |
Talk
09:47, 28 February 2007 (UTC)
- More comments: The combo above looks good, but the animations are not synchronized - but I don't know if that really matters. The linear could be drawn out a little, to fill the empty space in the upper left quadrant. --
Janke |
Talk
08:01, 1 March 2007 (UTC)
- They appear synchronized to me. Maybe it's your browser --
froth
T
23:44, 1 March 2007 (UTC)
- They can be asynchronous the first time you download the page, since animated gifs start immediately after downloading. The second time the files are already in your browser cache, so they should start synchronously. ~ trialsanderrors 21:46, 6 March 2007 (UTC)
- They appear synchronized to me. Maybe it's your browser --
froth
T
23:44, 1 March 2007 (UTC)
- More comments: The combo above looks good, but the animations are not synchronized - but I don't know if that really matters. The linear could be drawn out a little, to fill the empty space in the upper left quadrant. --
Janke |
Talk
08:01, 1 March 2007 (UTC)
Support combined version. Noclip 19:44, 28 February 2007 (UTC)
- Support trialsanderrors version. Noclip 03:56, 1 March 2007 (UTC)
- Comment I arranged the new versions in a table and Support that arrangement. ~ trialsanderrors 23:17, 28 February 2007 (UTC)
- Support the same-sized but separate images. Feature them all. -- froth T 23:44, 1 March 2007 (UTC)
- Comment - Please don't put the label "P1" over the segment - Alvesgaspar 21:47, 2 March 2007 (UTC)
- Strong support "All together now" version, wow, I am learning. HighInBC(Need help? Ask me) 19:11, 10 March 2007 (UTC)
- Oppose set, per my comment above - Alvesgaspar 13:07, 11 March 2007 (UTC)
- Support I support the combined image.-- Paul 17:50, 12 March 2007 (UTC)
- Q So is this going to be our first featured set? ~
trialsanderrors
17:32, 15 March 2007 (UTC)
- No, look at the description on
this page --
froth
t
18:49, 23 March 2007 (UTC)
- See the discussion and the new template on the talk page. ~ trialsanderrors 19:11, 23 March 2007 (UTC)
- No, look at the description on
this page --
froth
t
18:49, 23 March 2007 (UTC)
- Still support cubic. Higher order curves a rarely used. "Quadratic and cubic Bézier curves are most common; higher degree curves are more expensive to evaluate. When more complex shapes are needed, low order Bézier curves are patched together." ed g2s • talk 23:39, 19 March 2007 (UTC)
- Support as a set, the images are not used together in the article. -- KFP ( talk | contribs) 13:39, 28 March 2007 (UTC)
- Support the all-in-one version. Very, very nice. And what an excellent visualization. We need a lot more images like this. -- Cyde Weys 01:07, 1 April 2007 (UTC)
- Comment. The article where these images appear, Bézier curve, would probably have to be refactored if the combined version was promoted. -- KFP ( talk | contribs) 10:48, 2 April 2007 (UTC)
- Support. My preference is for the four curves to be promoted as a set but kept as separate images. One can be selected as representative of the set when it comes to Main Page appearances etc. Pstuart84 Talk 15:42, 2 April 2007 (UTC)
Promoted as a set, with Image:Bézier 3 big.gif as main image. -- KFP ( talk | contribs) 10:06, 3 April 2007 (UTC)
![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}{n \choose i}\mathbf {P} _{i}(1-t)^{n-i}t^{i}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0d697418271c2b9104a3a1af9c97d785a8bc441)