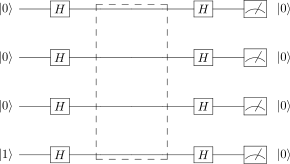
Circuits that provide a constant output of either ${\displaystyle |0\rangle }$ or ${\displaystyle |1\rangle }$ can be viewed as having the output qubit disconnected from the input qubits. It is therefore expected that the input qubits measure as ${\displaystyle |0\rangle ^{\otimes n}}$.

Output qubit is constant ${\displaystyle |0\rangle }$	Outputs qubit is constant ${\displaystyle |1\rangle }$

In the circuit diagrams, the functions are shown within a dashed line border. It is important to note that an ${\displaystyle X}$ gate that flips ${\displaystyle |0\rangle }$ to ${\displaystyle |1\rangle }$ has no effect in the Hadamard basis. ${\displaystyle |+\rangle }$ passes through an ${\displaystyle X}$ gate unchanged.

A sub-class of balanced functions uses only a single input qubit to decide whether the output qubit is ${\displaystyle |0\rangle }$ or ${\displaystyle |1\rangle }$.

Output qubit is the value of one input qubit	Output qubit is the negation of one input qubit

Separating the Bell State ${\displaystyle |\Phi ^{+}\rangle }$

When the CNOT gate acts upon two qubits that are perfectly correlated in the ${\displaystyle |\Phi ^{+}\rangle }$ state, the outputs are the unentangled states ${\displaystyle |+\rangle _{A}}$ and ${\displaystyle |0\rangle _{B}}$. The CNOT gate is its own inverse.

To demonstrate this, we show that in any chosen basis the perfect correlation and the operation of the CNOT gate combine to produce a constant output.

Selecting the computational basis ${\displaystyle \{|0\rangle ,|1\rangle \}}$ we have:

Qubit A's effect on qubit B

Based on qubit B correlating exactly with qubit A and then qubit B being subjected to the CNOT X-rotation depending on qubit A:

${\displaystyle |0\rangle _{A}}$ correlates to ${\displaystyle |0\rangle _{B}}$ which results in ${\displaystyle |0\rangle _{B}}$

${\displaystyle |1\rangle _{A}}$ correlates to ${\displaystyle |1\rangle _{B}}$ which results in ${\displaystyle |0\rangle _{B}}$

Qubit B's effect on qubit A

The basis vectors that we've chosen, represented by Hadamard basis vectors are:

${\displaystyle \{{\frac {1}{\sqrt {2}}}(|+\rangle +|-\rangle ),{\frac {1}{\sqrt {2}}}(|+\rangle -|-\rangle )\}}$

${\displaystyle {\frac {1}{\sqrt {2}}}(|+\rangle _{B}+|-\rangle _{B})}$

Separates into:

${\displaystyle {\frac {1}{2}}(|+\rangle _{A}+|-\rangle _{A})}$ and ${\displaystyle {\frac {1}{2}}(|-\rangle _{A}+|+\rangle _{A})}$

The other basis vector:

${\displaystyle {\frac {1}{\sqrt {2}}}(|+\rangle _{B}-|-\rangle _{B})}$

Separates into:

${\displaystyle {\frac {1}{2}}(|+\rangle _{A}-|-\rangle _{A})}$ and ${\displaystyle {\frac {-1}{2}}(|-\rangle _{A}-|+\rangle _{A})}$

So the resulting state of summing the results of the basis transformations (and dividing by 2) is the constant:

${\displaystyle |+\rangle _{A}}$

Further worked example

Using an arbitrarily-selected basis of: ${\displaystyle \{{\frac {1}{5}}(3|0\rangle +4|1\rangle ),{\frac {1}{5}}(3|1\rangle -4|0\rangle )\}}$

Qubit A's effect on qubit B

Based on qubit B correlating exactly with qubit A and then qubit B being subjected to the CNOT X-rotation depending on qubit A:

${\displaystyle {\frac {1}{5}}(3|0\rangle _{A}+4|1\rangle _{A})}$

Separates into:

${\displaystyle {\frac {3}{25}}(3|0\rangle _{B}+4|1\rangle _{B})}$ and ${\displaystyle {\frac {4}{25}}(3|1\rangle _{B}+4|0\rangle _{B})}$ which equals ${\displaystyle {\frac {25}{25}}|0\rangle _{B}+{\frac {24}{25}}|1\rangle _{B}}$

The other basis vector:

${\displaystyle {\frac {1}{5}}(3|1\rangle _{A}-4|0\rangle _{A})}$

Separates into:

${\displaystyle {\frac {3}{25}}(3|0\rangle _{B}-4|1\rangle _{B})}$ and ${\displaystyle {\frac {-4}{25}}(3|1\rangle _{B}-4|0\rangle _{B})}$ which equals ${\displaystyle {\frac {25}{25}}|0\rangle _{B}-{\frac {24}{25}}|1\rangle _{B}}$

So the resulting state of summing the results of the basis transformations (and dividing by 2) is the constant:

${\displaystyle |0\rangle _{B}}$

Qubit B's effect on qubit A

The basis vectors that we've chosen, represented by Hadamard basis vectors are: ${\displaystyle \{{\frac {1}{5{\sqrt {2}}}}(7|+\rangle -|-\rangle ),{\frac {-1}{5{\sqrt {2}}}}(|+\rangle +7|-\rangle )\}}$

${\displaystyle {\frac {1}{5{\sqrt {2}}}}(7|+\rangle _{B}-|-\rangle _{B})}$

Separates into:

${\displaystyle {\frac {7}{50}}(7|+\rangle _{A}-|-\rangle _{A})}$ and ${\displaystyle {\frac {-1}{50}}(7|-\rangle _{A}-|+\rangle _{A})}$ which equals ${\displaystyle {\frac {50}{50}}|+\rangle _{A}-{\frac {14}{50}}|-\rangle _{A}}$

The other basis vector:

${\displaystyle {\frac {-1}{5{\sqrt {2}}}}(|+\rangle _{B}+7|-\rangle _{B})}$

Separates into:

${\displaystyle {\frac {1}{50}}(|+\rangle _{A}+7|-\rangle _{A})}$ and ${\displaystyle {\frac {7}{50}}(|-\rangle _{A}+7|+\rangle _{A})}$ which equals ${\displaystyle {\frac {50}{50}}|+\rangle _{A}+{\frac {14}{50}}|-\rangle _{A}}$

So the resulting state of summing the results of the basis transformations (and dividing by 2) is the constant:

${\displaystyle |+\rangle _{A}}$

Bell basis

The four Bell states form a Bell basis. A perfect correlation between any two bases on the individual qubits can be described as a sum of Bell states. For example, ${\displaystyle {\frac {1}{\sqrt {2}}}(|0+\rangle +|1-\rangle )}$ is maximally entangled but not a Bell state; it represents a correlation between the bases ${\displaystyle b_{1}}$ and ${\displaystyle b_{2}=H.b_{1}}$. It can be rewritten as ${\displaystyle {\frac {1}{\sqrt {2}}}(|\Phi ^{-}\rangle +|\Psi ^{+}\rangle )}$ using Bell basis states. ^[a]

Fix issue

The overlap expression ${\displaystyle \langle \phi \mid \psi \rangle }$ is typically interpreted as the probability amplitude for the state \psi to collapse into the state \phi.

Notes