In the mathematical theory of reflection groups, the parabolic subgroups are a special kind of subgroup. The precise definition of which subgroups are parabolic depends on context—for example, whether one is discussing general Coxeter groups or complex reflection groups—but in all cases the collection of parabolic subgroups exhibits important good behaviors. For example, the parabolic subgroups of a reflection group have a natural indexing set and form a lattice when ordered by inclusion. The different definitions of parabolic subgroups essentially coincide in the case of finite real reflection groups. Parabolic subgroups arise in the theory of algebraic groups, through their connection with Weyl groups.
In a Euclidean space (such as the Euclidean plane, ordinary three-dimensional space, or higher-dimensional analogues), a reflection is a symmetry of the space across a mirror (technically, across a subspace of dimension one smaller than the whole space) that fixes the vectors that lie on the mirror and send the vectors orthogonal to the mirror to their negatives. A finite real reflection group W is a finite group generated by reflections (that is, every linear transformation in W is a composition of some of the reflections in W). [1] For example, the symmetries of a regular polygon in the plane form a reflection group (called the dihedral group), because each rotation symmetry of the polygon is a composition of two reflections. [2] Finite real reflection groups can be generalized in various ways, [3] and the definition of parabolic subgroup depends on the choice of definition.
Each finite real reflection group W has the structure of a Coxeter group: [1] this means that W contains a subset S of reflections (called simple reflections) such that S generates W, subject to relations of the form where 1 denotes the identity in W and the are numbers that satisfy for and for . [a] [4] Thus, the Coxeter groups form one generalization of finite real reflection groups.
A separate generalization is to consider the geometric action on vector spaces whose underlying field is not the real numbers. [1] Especially, if one replaces the real numbers with the complex numbers, with a corresponding generalization of the notion of a reflection, one arrives at the definition of a complex reflection group. [b] Every real reflection group can be complexified to give a complex reflection group, so the complex reflection groups form another generalization of finite real reflection groups. [6] [7]

Suppose that W is a Coxeter group with a finite set S of simple reflections. For each subset I of S, let denote the subgroup of W generated by . Such subgroups are called standard parabolic subgroups of W. [8] [9] In the extreme cases, is the trivial subgroup (containing just the identity element of W) and . [10]
The pair is again a Coxeter group. Moreover, the Coxeter group structure on is compatible with that on W, in the following sense: if denotes the length function on W with respect to S (so that if the element w of W can be written as a product of k elements of S and not fewer), then for every element w of , one has that . That is, the length of w is the same whether it is viewed as an element of W or of . [8] [9] The same is true of the Bruhat order: if u and w are elements of , then in the Bruhat order on if and only if in the Bruhat order on W. [11]
If I and J are two subsets of S, then if and only if , , and the smallest group that contains both and is . Consequently, the lattice of standard parabolic subgroups of W is a Boolean lattice. [8] [9]
Given a standard parabolic subgroup of a Coxeter group W, the cosets of in W have a particularly nice system of representatives: let denote the set of elements in W that do not have any element of I as a right descent. [c] Then for each , there are unique elements and such that . Moreover, this is a length-additive product, that is, . Furthermore, u is the element of minimum length in the coset . [8] [13] An analogous construction is valid for right cosets. [14] The collection of all left cosets of standard parabolic subgroups is one possible construction of the Coxeter complex. [15]
In terms of the Coxeter–Dynkin diagram, the standard parabolic subgroups arise by taking a subset of the nodes of the diagram and the edges induced between those nodes, erasing all others. [16] The only normal parabolic subgroups arise by taking a union of connected components of the diagram, and the whole group W is the direct product of the irreducible Coxeter groups that correspond to the components. [17]
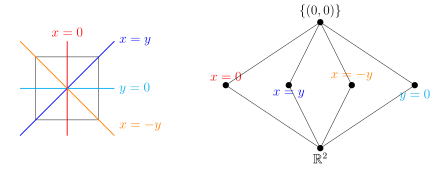
Suppose that W is a complex reflection group acting on a complex vector space V. For any subset , let be the subset of W consisting of those elements in W that fix each element of A. [d] Such a subgroup is called a parabolic subgroup of W. [19] In the extreme cases, and is the trivial subgroup of W that contains only the identity element.
It follows from a theorem of Steinberg (1964) that each parabolic subgroup of a complex reflection group W is a reflection group, generated by the reflections in W that fix every point in A. [20] Since W acts linearly on V, where is the span of A (that is, the smallest linear subspace of V that contains A). [19] In fact, there is a simple choice of subspaces A that index the parabolic subgroups: each reflection in W fixes a hyperplane (that is, a subspace of V whose dimension is 1 less than that of V) pointwise, and the collection of all these hyperplanes is the reflection arrangement of W. [21] The collection of all intersections of subsets of these hyperplanes, [e] partially ordered by inclusion, is a lattice . [22] The elements of the lattice are precisely the fixed spaces of the elements of W (that is, for each intersection I of reflecting hyperplanes, there is an element such that ). [23] [24] The map that sends for is an order-reversing bijection between subspaces in and parabolic subgroups of W. [24]
Let W be a finite real reflection group; that is, W is a finite group of linear transformations on a finite-dimensional real Euclidean space that is generated by orthogonal reflections. As mentioned above (see § Background: reflection groups), W may be viewed as both a Coxeter group and as a complex reflection group. For a real reflection group W, the parabolic subgroups of W (viewed as a complex reflection group) are not all standard parabolic subgroups of W (when viewed as a Coxeter group, after specifying a fixed Coxeter generating set S), as there are many more subspaces in the intersection lattice of its reflection arrangement than subsets of S. However, in a finite real reflection group W, every parabolic subgroup is conjugate to a standard parabolic subgroup with respect to S. [25]

4, represented as signed permutations of {−2, −1, 1, 2}, with identity ι
The symmetric group , which consists of all permutations of , is a Coxeter group with respect to the set of adjacent transpositions , ..., . The standard parabolic subgroups of (which are also known as Young subgroups) are the subgroups of the form , where are positive integers with sum n, in which the first factor in the direct product permutes the elements among themselves, the second factor permutes the elements among themselves, and so on. [26] [14]
The hyperoctahedral group , which consists of all signed permutations of (that is, the bijections w on that set such that for all i), has as its maximal standard parabolic subgroups the stabilizers of for . [27]
In a Coxeter group generated by a finite set S of simple reflections, one may define a parabolic subgroup to be any conjugate of a standard parabolic subgroup. Under this definition, it is still true that the intersection of any two parabolic subgroups is a parabolic subgroup. The same does not hold in general for Coxeter groups of infinite rank. [28]
If W is a group and T is a subset of W, the pair is called a dual Coxeter system if there exists a subset S of T such that is a Coxeter system and so that T is the set of all reflections (conjugates of the simple reflections) in W. For a dual Coxeter system , a subgroup of W is said to be a parabolic subgroup if it is a standard parabolic (as in § In Coxeter groups) of for some choice of simple reflections S for . [29] [f]
In some dual Coxeter systems, all sets of simple reflections are conjugate to each other; in this case, the parabolic subgroups with respect to one simple system (that is, the conjugates of the standard parabolic subgroups) coincide with the parabolic subgroups with respect to any other simple system. However, even in finite examples, this may not hold: for example, if W is the dihedral group with 10 elements, viewed as symmetries of a regular pentagon, and T is the set of reflection symmetries of the polygon, then any pair of reflections in T forms a simple system for , but not all pairs of reflections are conjugate to each other. [29] Nevertheless, if W is finite, then the parabolic subgroups (in the sense above) coincide with the parabolic subgroups in the classical sense (that is, the conjugates of the standard parabolic subgroups with respect to a single, fixed, choice of simple reflections S). [31] The same result does not hold in general for infinite Coxeter groups. [32]
When W is an affine Coxeter group, the associated finite Weyl group is always a maximal parabolic subgroup, whose Coxeter–Dynkin diagram is the result of removing one node from the diagram of W. In particular, the length functions on the finite and affine groups coincide. [33] In fact, every standard parabolic subgroup of an affine Coxeter group is finite. [34] As in the case of finite real reflection groups, when we consider the action of an affine Coxeter group W on a Euclidean space V, the conjugates of the standard parabolic subgroups of W are precisely the subgroups of the form for some subset A of V. [35]
If W is a crystallographic Coxeter group, [g] then every parabolic subgroup of W is also crystallographic. [36]
If G is an algebraic group and B is a Borel subgroup for G, then a parabolic subgroup of G is any subgroup that contains B. [h] If furthermore G has a (B, N) pair, then the associated quotient group is a Coxeter group, called the Weyl group of G. Then the group G has a Bruhat decomposition into double cosets (where is the disjoint union), and the parabolic subgroups of G containing B are precisely the subgroups of the form where is a standard parabolic subgroup of W. [39]
Suppose W is a Coxeter group of finite rank (that is, the set S of simple generators is finite). Given any subset X of W, one may define the parabolic closure of X to be the intersection of all parabolic subgroups containing X. As mentioned above, in this case the intersection of any two parabolic subgroups of W is again a parabolic subgroup of W, and consequently the parabolic closure of X is a parabolic subgroup of W; in particular, it is the (unique) minimal parabolic subgroup of W containing X. [28] The same analysis applies to complex reflection groups, where the parabolic closure of X is also the pointwise stabiliser of the space of fixed points of X. [40] The same does not hold for Coxeter groups of infinite rank. [28]
Each Coxeter group is associated to another group called its Artin–Tits group or generalized braid group, which is defined by omitting the relations for each generator from its Coxeter presentation. [i] [41] Although generalized braid groups are not reflection groups, they inherit a notion of parabolic subgroups: a standard parabolic subgroup of a generalized braid group is a subgroup generated by a subset of the standard generating set S, and a parabolic subgroup is any subgroup conjugate to a standard parabolic. [42]
A generalized braid group is said to be of spherical type if the associated Coxeter group is finite. If B is a generalized braid group of spherical type, then the intersection of any two parabolic subgroups of B is also a parabolic subgroup. Consequently, the parabolic subgroups of B form a lattice under inclusion. [42]
For a finite real reflection group W, the associated generalized braid group may be defined in purely topological language, without referring to a particular group presentation. [j] This definition naturally extends to finite complex reflection groups. [43] Parabolic subgroups can also be defined in this setting. [44]
- ^ In general Coxeter groups, the possibility is also allowed, meaning that no relation holds between s and s'—but this situation cannot occur in a finite group.
- ^ Such groups are also known as unitary reflection groups or complex pseudo-reflection groups in some sources. Similarly, sometimes complex reflections (linear transformations that fix a hyperplane pointwise) are called pseudo-reflections. [5]
- ^ A right descent of an element w in a Coxeter group is a simple reflection s such that . [12]
- ^ Sometimes such subgroups are called isotropy groups. [18]
- ^ Including the entire space V, as the empty intersection.
- ^ In the case of a finite real reflection group, this definition differs from the classical one, where S necessarily comes from the reflections whose reflecting hyperplanes form the boundaries of a chamber. [30]
- ^ That is, if W is a (possibly infinite) Coxeter group that stabilizes a lattice in its natural geometric representation.
- ^ This use of the phrase "parabolic subgroup" was introduced by Roger Godement in his paper Godement (1961). [37] [38]
- ^ The name "generalized braid group" arises from the fact that, in the special case is the symmetric group, the associated Artin–Tits group is the braid group on n strands.
- ^ In particular, the group W acts on the complement of the complexification of the arrangement of its reflecting hyperplanes; the generalized braid group of W is the fundamental group of the quotient of this space under the action of W.
- ^ a b c Kane (2001), p. 1.
- ^ Kane (2001), pp. 8–14.
- ^ Humphreys (1990), pp. xi–xii.
- ^ Humphreys (1990), §1.9.
- ^ Kane (2001), p. 160.
- ^ Lehrer & Taylor (2009), p. 1.
- ^ Humphreys (1990), p. 66.
- ^ a b c d Björner & Brenti (2005), §2.4.
- ^ a b c Humphreys (1990), §5.5.
- ^ Humphreys (1990), §1.10.
- ^ Humphreys (1990), §5.10.
- ^ Björner & Brenti (2005), p. 17.
- ^ Humphreys (1990), §5.12.
- ^ a b Björner & Brenti (2005), p. 41.
- ^ Björner & Brenti (2005), pp. 86–7.
- ^ Björner & Brenti (2005), p. 39.
- ^ Humphreys (1990), pp. 118, 129.
- ^ Kane (2001), p. 60.
- ^ a b Lehrer & Taylor (2009), p. 171.
- ^ Lehrer & Taylor (2009), §9.7.
- ^ Orlik & Terao (1992), p. 215.
- ^ Orlik & Terao (1992), §2.1.
- ^ Lehrer & Taylor (2009), §9.3.
- ^ a b Broué (2010), §4.2.4.
- ^ Kane (2001), §5.2.
- ^ Kane (2001), p. 58.
- ^ Björner & Brenti (2005), p. 248.
- ^ a b c Nuida (2012).
- ^ a b Baumeister et al. (2014).
- ^ Reiner, Ripoll & Stump (2017), Example 1.2.
- ^ Baumeister et al. (2017), Proposition 1.4 and Corollary 4.4.
- ^ Gobet (2017), Example 2.2.
- ^ Humphreys (1990), p. 114.
- ^ Humphreys (1990), p. 96.
- ^ Kane (2001), p. 130.
- ^ Humphreys (1990), p. 136.
- ^ Borel (2001), chapter VI, section 2.
- ^ Chow (2010).
- ^ Digne & Michel (1991), pp. 19–21.
- ^ Taylor (2012).
- ^ McCammond & Sulway (2017).
- ^ a b Cumplido et al. (2019).
- ^ Broué (2010), §4.2.5.
- ^ González-Meneses & Marin (2022).
- Baumeister, Barbara; Dyer, Matthew; Stump, Christian; Wegener, Patrick (2014), "A note on the transitive Hurwitz action on decompositions of parabolic Coxeter elements", Proceedings of the American Mathematical Society, Series B, 1 (13): 149–154, arXiv: 1402.2500, doi: 10.1090/S2330-1511-2014-00017-1
- Baumeister, Barbara; Gobet, Thomas; Roberts, Kieran; Wegener, Patrick (2017), "On the Hurwitz action in finite Coxeter groups", J. Group Theory, 20 (1): 103–131, arXiv: 1512.04764, doi: 10.1515/jgth-2016-0025, S2CID 44035800
- Björner, Anders; Brenti, Francesco (2005), Combinatorics of Coxeter groups, Springer, doi: 10.1007/3-540-27596-7, ISBN 978-3540-442387, S2CID 115235335
- Borel, Armand (2001), Essays in the history of Lie groups and algebraic groups, History of Mathematics, vol. 21, American Mathematical Society and London Mathematical Society, ISBN 0-8218-0288-7
- Broué, Michel (2010), Introduction to Complex Reflection Groups and Their Braid Groups, Lecture Notes in Mathematics, vol. 1988, Springer-Verlag, doi: 10.1007/978-3-642-11175-4, ISBN 978-3-642-11174-7
- Chow, Timothy (2010), "Why are parabolic subgroups called "parabolic subgroups"?", MathOverflow, et al., retrieved 2024-02-16
- Cumplido, María; Gebhardt, Volker; González-Meneses, Juan; Wiest, Bert (2019), "On parabolic subgroups of Artin–Tits groups of spherical type", Advances in Mathematics, 352: 572–610, arXiv: 1712.06727, doi: 10.1016/j.aim.2019.06.010
- Digne, François; Michel, Jean (1991), Representations of finite groups of Lie type, London Mathematical Society Student Texts, vol. 21, Cambridge University Press, ISBN 0-521-40117-8
- Gobet, Thomas (2017), "On cycle decompositions in Coxeter groups", Sém. Lothar. Combin., 78B: Art. 45, arXiv: 1611.03442
- Godement, Roger (1961), "Groupes linéaires algébriques sur un corps parfait", Sémin. Bourbaki, 13
- González-Meneses, Juan; Marin, Ivan (2022), Parabolic subgroups of complex braid groups I, arXiv: 2208.11938v1
- Humphreys, James E. (1990), Reflection groups and Coxeter groups, Cambridge University Press, doi: 10.1017/CBO9780511623646, ISBN 0-521-37510-X, S2CID 121077209
- Kane, Richard (2001), Reflection groups and invariant theory, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi: 10.1007/978-1-4757-3542-0, ISBN 0-387-98979-X, S2CID 119694827
- Lehrer, Gustav I.; Taylor, Donald E. (2009), Unitary reflection groups, Australian Mathematical Society Lecture Series, vol. 20, Cambridge University Press, ISBN 978-0-521-74989-3
- McCammond, Jon; Sulway, Robert (2017), "Artin groups of Euclidean type", Invent. Math., 210 (1): 231–282, arXiv: 1312.7770, Bibcode: 2017InMat.210..231M, doi: 10.1007/s00222-017-0728-2, S2CID 253738806
- Nuida, Koji (2012), "Locally parabolic subgroups in Coxeter groups of arbitrary ranks", Journal of Algebra, 350: 207–217, arXiv: 1006.4709, doi: 10.1016/j.jalgebra.2011.11.005
- Orlik, Peter; Terao, Hiroaki (1992), Arrangements of Hyperplanes, Grundlehren der mathematischen Wissenschaften, Springer, doi: 10.1007/978-3-662-02772-1, ISBN 978-3-540-55259-8
- Reiner, Victor; Ripoll, Vivien; Stump, Christian (2017), "On non-conjugate Coxeter elements in well-generated reflection groups", Math. Z., 285 (3–4): 1041–1062, arXiv: 1404.5522, doi: 10.1007/s00209-016-1736-4, S2CID 253752187
- Steinberg, Robert (1964), "Differential equations invariant under finite reflection groups", Transactions of the American Mathematical Society, 112 (3): 392–400, doi: 10.1090/S0002-9947-1964-0167535-3
- Taylor, D.E. (2012), "Reflection subgroups of finite complex reflection groups", Journal of Algebra, 366: 218–234, arXiv: 1201.1348, doi: 10.1016/j.jalgebra.2012.04.033
In the mathematical theory of reflection groups, the parabolic subgroups are a special kind of subgroup. The precise definition of which subgroups are parabolic depends on context—for example, whether one is discussing general Coxeter groups or complex reflection groups—but in all cases the collection of parabolic subgroups exhibits important good behaviors. For example, the parabolic subgroups of a reflection group have a natural indexing set and form a lattice when ordered by inclusion. The different definitions of parabolic subgroups essentially coincide in the case of finite real reflection groups. Parabolic subgroups arise in the theory of algebraic groups, through their connection with Weyl groups.
In a Euclidean space (such as the Euclidean plane, ordinary three-dimensional space, or higher-dimensional analogues), a reflection is a symmetry of the space across a mirror (technically, across a subspace of dimension one smaller than the whole space) that fixes the vectors that lie on the mirror and send the vectors orthogonal to the mirror to their negatives. A finite real reflection group W is a finite group generated by reflections (that is, every linear transformation in W is a composition of some of the reflections in W). [1] For example, the symmetries of a regular polygon in the plane form a reflection group (called the dihedral group), because each rotation symmetry of the polygon is a composition of two reflections. [2] Finite real reflection groups can be generalized in various ways, [3] and the definition of parabolic subgroup depends on the choice of definition.
Each finite real reflection group W has the structure of a Coxeter group: [1] this means that W contains a subset S of reflections (called simple reflections) such that S generates W, subject to relations of the form where 1 denotes the identity in W and the are numbers that satisfy for and for . [a] [4] Thus, the Coxeter groups form one generalization of finite real reflection groups.
A separate generalization is to consider the geometric action on vector spaces whose underlying field is not the real numbers. [1] Especially, if one replaces the real numbers with the complex numbers, with a corresponding generalization of the notion of a reflection, one arrives at the definition of a complex reflection group. [b] Every real reflection group can be complexified to give a complex reflection group, so the complex reflection groups form another generalization of finite real reflection groups. [6] [7]

Suppose that W is a Coxeter group with a finite set S of simple reflections. For each subset I of S, let denote the subgroup of W generated by . Such subgroups are called standard parabolic subgroups of W. [8] [9] In the extreme cases, is the trivial subgroup (containing just the identity element of W) and . [10]
The pair is again a Coxeter group. Moreover, the Coxeter group structure on is compatible with that on W, in the following sense: if denotes the length function on W with respect to S (so that if the element w of W can be written as a product of k elements of S and not fewer), then for every element w of , one has that . That is, the length of w is the same whether it is viewed as an element of W or of . [8] [9] The same is true of the Bruhat order: if u and w are elements of , then in the Bruhat order on if and only if in the Bruhat order on W. [11]
If I and J are two subsets of S, then if and only if , , and the smallest group that contains both and is . Consequently, the lattice of standard parabolic subgroups of W is a Boolean lattice. [8] [9]
Given a standard parabolic subgroup of a Coxeter group W, the cosets of in W have a particularly nice system of representatives: let denote the set of elements in W that do not have any element of I as a right descent. [c] Then for each , there are unique elements and such that . Moreover, this is a length-additive product, that is, . Furthermore, u is the element of minimum length in the coset . [8] [13] An analogous construction is valid for right cosets. [14] The collection of all left cosets of standard parabolic subgroups is one possible construction of the Coxeter complex. [15]
In terms of the Coxeter–Dynkin diagram, the standard parabolic subgroups arise by taking a subset of the nodes of the diagram and the edges induced between those nodes, erasing all others. [16] The only normal parabolic subgroups arise by taking a union of connected components of the diagram, and the whole group W is the direct product of the irreducible Coxeter groups that correspond to the components. [17]
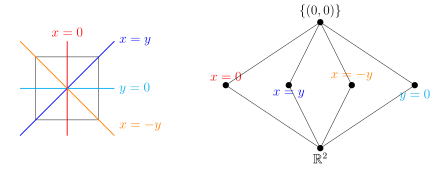
Suppose that W is a complex reflection group acting on a complex vector space V. For any subset , let be the subset of W consisting of those elements in W that fix each element of A. [d] Such a subgroup is called a parabolic subgroup of W. [19] In the extreme cases, and is the trivial subgroup of W that contains only the identity element.
It follows from a theorem of Steinberg (1964) that each parabolic subgroup of a complex reflection group W is a reflection group, generated by the reflections in W that fix every point in A. [20] Since W acts linearly on V, where is the span of A (that is, the smallest linear subspace of V that contains A). [19] In fact, there is a simple choice of subspaces A that index the parabolic subgroups: each reflection in W fixes a hyperplane (that is, a subspace of V whose dimension is 1 less than that of V) pointwise, and the collection of all these hyperplanes is the reflection arrangement of W. [21] The collection of all intersections of subsets of these hyperplanes, [e] partially ordered by inclusion, is a lattice . [22] The elements of the lattice are precisely the fixed spaces of the elements of W (that is, for each intersection I of reflecting hyperplanes, there is an element such that ). [23] [24] The map that sends for is an order-reversing bijection between subspaces in and parabolic subgroups of W. [24]
Let W be a finite real reflection group; that is, W is a finite group of linear transformations on a finite-dimensional real Euclidean space that is generated by orthogonal reflections. As mentioned above (see § Background: reflection groups), W may be viewed as both a Coxeter group and as a complex reflection group. For a real reflection group W, the parabolic subgroups of W (viewed as a complex reflection group) are not all standard parabolic subgroups of W (when viewed as a Coxeter group, after specifying a fixed Coxeter generating set S), as there are many more subspaces in the intersection lattice of its reflection arrangement than subsets of S. However, in a finite real reflection group W, every parabolic subgroup is conjugate to a standard parabolic subgroup with respect to S. [25]

4, represented as signed permutations of {−2, −1, 1, 2}, with identity ι
The symmetric group , which consists of all permutations of , is a Coxeter group with respect to the set of adjacent transpositions , ..., . The standard parabolic subgroups of (which are also known as Young subgroups) are the subgroups of the form , where are positive integers with sum n, in which the first factor in the direct product permutes the elements among themselves, the second factor permutes the elements among themselves, and so on. [26] [14]
The hyperoctahedral group , which consists of all signed permutations of (that is, the bijections w on that set such that for all i), has as its maximal standard parabolic subgroups the stabilizers of for . [27]
In a Coxeter group generated by a finite set S of simple reflections, one may define a parabolic subgroup to be any conjugate of a standard parabolic subgroup. Under this definition, it is still true that the intersection of any two parabolic subgroups is a parabolic subgroup. The same does not hold in general for Coxeter groups of infinite rank. [28]
If W is a group and T is a subset of W, the pair is called a dual Coxeter system if there exists a subset S of T such that is a Coxeter system and so that T is the set of all reflections (conjugates of the simple reflections) in W. For a dual Coxeter system , a subgroup of W is said to be a parabolic subgroup if it is a standard parabolic (as in § In Coxeter groups) of for some choice of simple reflections S for . [29] [f]
In some dual Coxeter systems, all sets of simple reflections are conjugate to each other; in this case, the parabolic subgroups with respect to one simple system (that is, the conjugates of the standard parabolic subgroups) coincide with the parabolic subgroups with respect to any other simple system. However, even in finite examples, this may not hold: for example, if W is the dihedral group with 10 elements, viewed as symmetries of a regular pentagon, and T is the set of reflection symmetries of the polygon, then any pair of reflections in T forms a simple system for , but not all pairs of reflections are conjugate to each other. [29] Nevertheless, if W is finite, then the parabolic subgroups (in the sense above) coincide with the parabolic subgroups in the classical sense (that is, the conjugates of the standard parabolic subgroups with respect to a single, fixed, choice of simple reflections S). [31] The same result does not hold in general for infinite Coxeter groups. [32]
When W is an affine Coxeter group, the associated finite Weyl group is always a maximal parabolic subgroup, whose Coxeter–Dynkin diagram is the result of removing one node from the diagram of W. In particular, the length functions on the finite and affine groups coincide. [33] In fact, every standard parabolic subgroup of an affine Coxeter group is finite. [34] As in the case of finite real reflection groups, when we consider the action of an affine Coxeter group W on a Euclidean space V, the conjugates of the standard parabolic subgroups of W are precisely the subgroups of the form for some subset A of V. [35]
If W is a crystallographic Coxeter group, [g] then every parabolic subgroup of W is also crystallographic. [36]
If G is an algebraic group and B is a Borel subgroup for G, then a parabolic subgroup of G is any subgroup that contains B. [h] If furthermore G has a (B, N) pair, then the associated quotient group is a Coxeter group, called the Weyl group of G. Then the group G has a Bruhat decomposition into double cosets (where is the disjoint union), and the parabolic subgroups of G containing B are precisely the subgroups of the form where is a standard parabolic subgroup of W. [39]
Suppose W is a Coxeter group of finite rank (that is, the set S of simple generators is finite). Given any subset X of W, one may define the parabolic closure of X to be the intersection of all parabolic subgroups containing X. As mentioned above, in this case the intersection of any two parabolic subgroups of W is again a parabolic subgroup of W, and consequently the parabolic closure of X is a parabolic subgroup of W; in particular, it is the (unique) minimal parabolic subgroup of W containing X. [28] The same analysis applies to complex reflection groups, where the parabolic closure of X is also the pointwise stabiliser of the space of fixed points of X. [40] The same does not hold for Coxeter groups of infinite rank. [28]
Each Coxeter group is associated to another group called its Artin–Tits group or generalized braid group, which is defined by omitting the relations for each generator from its Coxeter presentation. [i] [41] Although generalized braid groups are not reflection groups, they inherit a notion of parabolic subgroups: a standard parabolic subgroup of a generalized braid group is a subgroup generated by a subset of the standard generating set S, and a parabolic subgroup is any subgroup conjugate to a standard parabolic. [42]
A generalized braid group is said to be of spherical type if the associated Coxeter group is finite. If B is a generalized braid group of spherical type, then the intersection of any two parabolic subgroups of B is also a parabolic subgroup. Consequently, the parabolic subgroups of B form a lattice under inclusion. [42]
For a finite real reflection group W, the associated generalized braid group may be defined in purely topological language, without referring to a particular group presentation. [j] This definition naturally extends to finite complex reflection groups. [43] Parabolic subgroups can also be defined in this setting. [44]
- ^ In general Coxeter groups, the possibility is also allowed, meaning that no relation holds between s and s'—but this situation cannot occur in a finite group.
- ^ Such groups are also known as unitary reflection groups or complex pseudo-reflection groups in some sources. Similarly, sometimes complex reflections (linear transformations that fix a hyperplane pointwise) are called pseudo-reflections. [5]
- ^ A right descent of an element w in a Coxeter group is a simple reflection s such that . [12]
- ^ Sometimes such subgroups are called isotropy groups. [18]
- ^ Including the entire space V, as the empty intersection.
- ^ In the case of a finite real reflection group, this definition differs from the classical one, where S necessarily comes from the reflections whose reflecting hyperplanes form the boundaries of a chamber. [30]
- ^ That is, if W is a (possibly infinite) Coxeter group that stabilizes a lattice in its natural geometric representation.
- ^ This use of the phrase "parabolic subgroup" was introduced by Roger Godement in his paper Godement (1961). [37] [38]
- ^ The name "generalized braid group" arises from the fact that, in the special case is the symmetric group, the associated Artin–Tits group is the braid group on n strands.
- ^ In particular, the group W acts on the complement of the complexification of the arrangement of its reflecting hyperplanes; the generalized braid group of W is the fundamental group of the quotient of this space under the action of W.
- ^ a b c Kane (2001), p. 1.
- ^ Kane (2001), pp. 8–14.
- ^ Humphreys (1990), pp. xi–xii.
- ^ Humphreys (1990), §1.9.
- ^ Kane (2001), p. 160.
- ^ Lehrer & Taylor (2009), p. 1.
- ^ Humphreys (1990), p. 66.
- ^ a b c d Björner & Brenti (2005), §2.4.
- ^ a b c Humphreys (1990), §5.5.
- ^ Humphreys (1990), §1.10.
- ^ Humphreys (1990), §5.10.
- ^ Björner & Brenti (2005), p. 17.
- ^ Humphreys (1990), §5.12.
- ^ a b Björner & Brenti (2005), p. 41.
- ^ Björner & Brenti (2005), pp. 86–7.
- ^ Björner & Brenti (2005), p. 39.
- ^ Humphreys (1990), pp. 118, 129.
- ^ Kane (2001), p. 60.
- ^ a b Lehrer & Taylor (2009), p. 171.
- ^ Lehrer & Taylor (2009), §9.7.
- ^ Orlik & Terao (1992), p. 215.
- ^ Orlik & Terao (1992), §2.1.
- ^ Lehrer & Taylor (2009), §9.3.
- ^ a b Broué (2010), §4.2.4.
- ^ Kane (2001), §5.2.
- ^ Kane (2001), p. 58.
- ^ Björner & Brenti (2005), p. 248.
- ^ a b c Nuida (2012).
- ^ a b Baumeister et al. (2014).
- ^ Reiner, Ripoll & Stump (2017), Example 1.2.
- ^ Baumeister et al. (2017), Proposition 1.4 and Corollary 4.4.
- ^ Gobet (2017), Example 2.2.
- ^ Humphreys (1990), p. 114.
- ^ Humphreys (1990), p. 96.
- ^ Kane (2001), p. 130.
- ^ Humphreys (1990), p. 136.
- ^ Borel (2001), chapter VI, section 2.
- ^ Chow (2010).
- ^ Digne & Michel (1991), pp. 19–21.
- ^ Taylor (2012).
- ^ McCammond & Sulway (2017).
- ^ a b Cumplido et al. (2019).
- ^ Broué (2010), §4.2.5.
- ^ González-Meneses & Marin (2022).
- Baumeister, Barbara; Dyer, Matthew; Stump, Christian; Wegener, Patrick (2014), "A note on the transitive Hurwitz action on decompositions of parabolic Coxeter elements", Proceedings of the American Mathematical Society, Series B, 1 (13): 149–154, arXiv: 1402.2500, doi: 10.1090/S2330-1511-2014-00017-1
- Baumeister, Barbara; Gobet, Thomas; Roberts, Kieran; Wegener, Patrick (2017), "On the Hurwitz action in finite Coxeter groups", J. Group Theory, 20 (1): 103–131, arXiv: 1512.04764, doi: 10.1515/jgth-2016-0025, S2CID 44035800
- Björner, Anders; Brenti, Francesco (2005), Combinatorics of Coxeter groups, Springer, doi: 10.1007/3-540-27596-7, ISBN 978-3540-442387, S2CID 115235335
- Borel, Armand (2001), Essays in the history of Lie groups and algebraic groups, History of Mathematics, vol. 21, American Mathematical Society and London Mathematical Society, ISBN 0-8218-0288-7
- Broué, Michel (2010), Introduction to Complex Reflection Groups and Their Braid Groups, Lecture Notes in Mathematics, vol. 1988, Springer-Verlag, doi: 10.1007/978-3-642-11175-4, ISBN 978-3-642-11174-7
- Chow, Timothy (2010), "Why are parabolic subgroups called "parabolic subgroups"?", MathOverflow, et al., retrieved 2024-02-16
- Cumplido, María; Gebhardt, Volker; González-Meneses, Juan; Wiest, Bert (2019), "On parabolic subgroups of Artin–Tits groups of spherical type", Advances in Mathematics, 352: 572–610, arXiv: 1712.06727, doi: 10.1016/j.aim.2019.06.010
- Digne, François; Michel, Jean (1991), Representations of finite groups of Lie type, London Mathematical Society Student Texts, vol. 21, Cambridge University Press, ISBN 0-521-40117-8
- Gobet, Thomas (2017), "On cycle decompositions in Coxeter groups", Sém. Lothar. Combin., 78B: Art. 45, arXiv: 1611.03442
- Godement, Roger (1961), "Groupes linéaires algébriques sur un corps parfait", Sémin. Bourbaki, 13
- González-Meneses, Juan; Marin, Ivan (2022), Parabolic subgroups of complex braid groups I, arXiv: 2208.11938v1
- Humphreys, James E. (1990), Reflection groups and Coxeter groups, Cambridge University Press, doi: 10.1017/CBO9780511623646, ISBN 0-521-37510-X, S2CID 121077209
- Kane, Richard (2001), Reflection groups and invariant theory, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer-Verlag, doi: 10.1007/978-1-4757-3542-0, ISBN 0-387-98979-X, S2CID 119694827
- Lehrer, Gustav I.; Taylor, Donald E. (2009), Unitary reflection groups, Australian Mathematical Society Lecture Series, vol. 20, Cambridge University Press, ISBN 978-0-521-74989-3
- McCammond, Jon; Sulway, Robert (2017), "Artin groups of Euclidean type", Invent. Math., 210 (1): 231–282, arXiv: 1312.7770, Bibcode: 2017InMat.210..231M, doi: 10.1007/s00222-017-0728-2, S2CID 253738806
- Nuida, Koji (2012), "Locally parabolic subgroups in Coxeter groups of arbitrary ranks", Journal of Algebra, 350: 207–217, arXiv: 1006.4709, doi: 10.1016/j.jalgebra.2011.11.005
- Orlik, Peter; Terao, Hiroaki (1992), Arrangements of Hyperplanes, Grundlehren der mathematischen Wissenschaften, Springer, doi: 10.1007/978-3-662-02772-1, ISBN 978-3-540-55259-8
- Reiner, Victor; Ripoll, Vivien; Stump, Christian (2017), "On non-conjugate Coxeter elements in well-generated reflection groups", Math. Z., 285 (3–4): 1041–1062, arXiv: 1404.5522, doi: 10.1007/s00209-016-1736-4, S2CID 253752187
- Steinberg, Robert (1964), "Differential equations invariant under finite reflection groups", Transactions of the American Mathematical Society, 112 (3): 392–400, doi: 10.1090/S0002-9947-1964-0167535-3
- Taylor, D.E. (2012), "Reflection subgroups of finite complex reflection groups", Journal of Algebra, 366: 218–234, arXiv: 1201.1348, doi: 10.1016/j.jalgebra.2012.04.033
































































